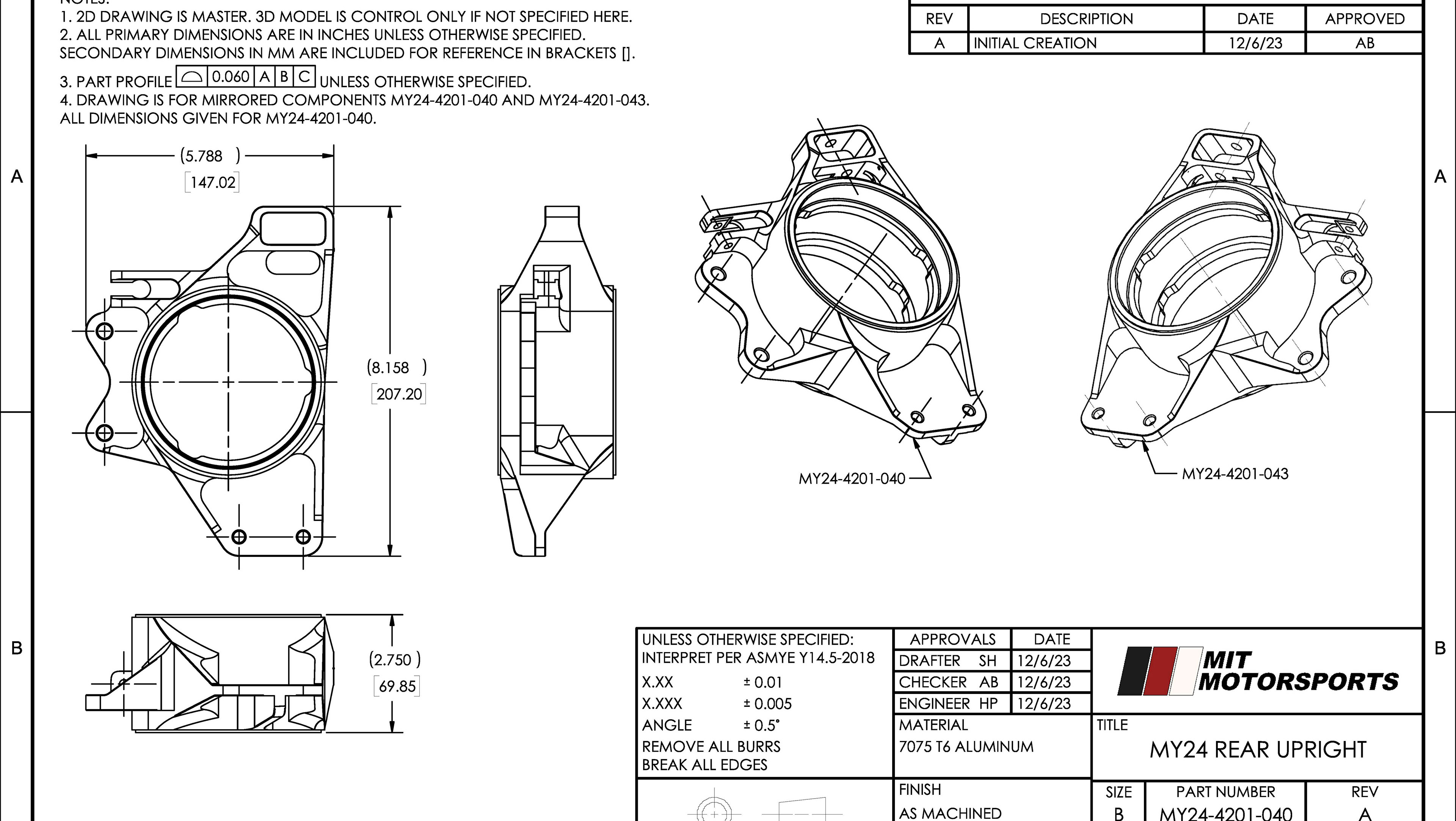
My primary role for the my24 car with MIt motorsports has been developing the braking system. Our system uses two independent hydraulic loops to operate the front and rear calipers respectively. I started by laying out the design requirements for the system including thermal and force requirements, relevant rules from the FSAE competition, and ease of manufacturing and assembly requirements. once those were established i examined numerous different architecture decisions such as caliper and master cylinder choices and brake rotor material, slot pattern, and mounting designs.
One of the key aspects of the design choices was determining the optimal brake balance between front and rear to account for the dive of the car under braking. To do this, I calculated what the optimal balance of front and rear weight distribution would be to achieve maximum possible deceleration. I did this with free body diagram analysis, using two equations derived from the forces acting upon the car in a simplified two-wheeled model. I took a moment balance about the center of mass of the car to find the equilibrium point of weight distribution, as well as using newton's second law to determine acceleration from the longitudinal forces applied by the tires.
Both of these equations were dependent on the percentage of the total car weight on the front tire, expressed as the variable r. i wrote a matlab script to iterate through all possible values of r to find the optimal weight distribution to maximize the acceleration. Below are segments of my matlab script that carried out the calculations.
We start by defining the characteristics of the car, including the position and mass of the center of mass, aerodynamic forces, and dimensions of the tires and brake rotors for torque calculations.
We then create an array of possible values of r (front weight percentage), and the associated values of acceleration from the moment balance and second law equations, finding the r that produces the maximum possible acceleration satisfying both equations.
This output graph shows how acceleration varies with r for both the moment balance and second law models. the optimal value of r is where the graphs intersect, at an r of 0.7404, or roughly 74% of the force rests on the front tires under braking.
Once we know the optimal brake ratio to target, we can find the optimal bore sizes for the front and rear master cylinders to hit that ratio by accumulating a list of commonly available master cylinder sizes and checking every possible combination to find the best two. The optimal bores are determined to be a 15mm front and 25.4mm rear cylinder bore. this gives us a brake bias of 0.7414, meaning we are only 0.1 percentage points off of the optimal ratio, which can easily be corrected with a slight bias bar adjustment.
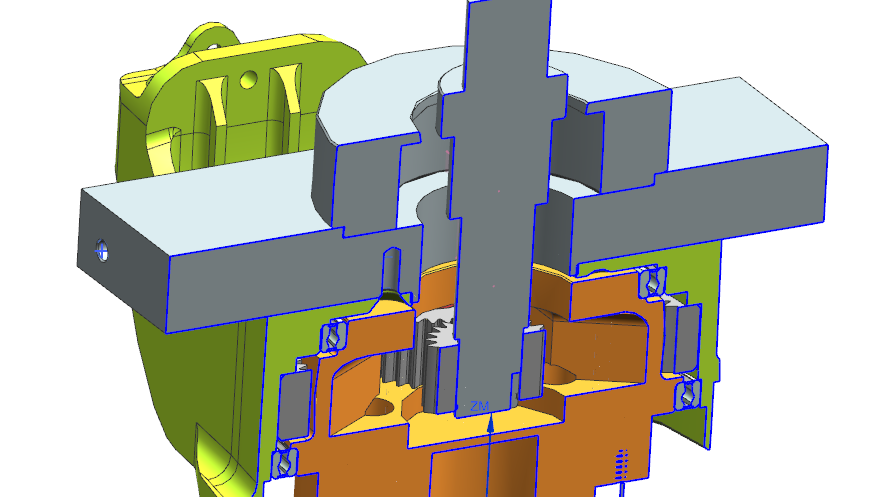
The main design constraint of the rotor itself is ensuring it can withstand the loads put on it without failing, even as the material weakens as the rotor heats up to close to 500 degrees Celsius. I performed structural analysis on the rotor by assembling a spreadsheet of calculations to analyze the tension, shear, and von mises stress at key points throughout the rotor and verify that stress did not exceed the material's capacity with a 1.5 factor of safety. The key areas I analyzed were the mounting tabs, the inner ring connecting the tabs, the spokes connecting the inner and outer ring, and the outer ring where the caliper grabs the rotor.
To the left is the CAD model of the rotor from NX. The tabs are symmetrical to allow the rotor to be mounted on the left or right side of the car while keeping the slanted spokes in the correct direction. The slanted spokes allow most of the load passing through them to be taken in tension, where steel is much stronger than in shear. The holes reduce the mass of the rotor while maximizing its surface area, decreasing its thermal mass and resistivity allowing it to cool much faster.
This is an example of the calculations performed to determine the necessary size of the various components of the rotor. This was analyzing the sizing of the mounting tabs to ensure they would not fail in shear when taking up the load from the calipers. Values listed at the top are the input parameters such as the material properties of the steel and the input forces from the caliper. The outputs listed below are the reaction forces produced in the tabs from the load and the necessary sizing of the tabs to support that load.
An example of a free body diagram that drives the analysis used in the spreadsheet. The tabs are arranged in 60 degree intervals for 6 tabs around the inner circumference. For the start of the analysis we assume the two supports closes to the caliper act as one support to simplify the equation, then spread the load from that virtual support across the two evenly spaced tabs. We assume the load is entirely borne by this one virtual support to be overly conservative and safe. in reality the load is shared across all six supports to varying degrees, but an error in the math on that spread could result in a tab getting overloaded and failing.
The machined rotors before getting surface ground being test fit on the hub. The mounting tabs fit exactly with no perceptible movement in the slots. The angle of the tabs allows the rotor to expand when heated without creating any gaps that would add shake and induce shock loading. As the rotor expands the tabs move radially outward, while also growing circumferentially to fill the wider space they now occupy.
The rotors mounted on the full wheel package. The outer ring has experienced some thermal bluing indicating the high temperatures hit during hard running. The banana-shaped tabs bolted into the hubs constrain the rotor axially while allowing a small amount of play to account for thermal expansion.
This system ran for over 400KM of driving on the MY24 car across four months of testing and two competitions. The rotors showed no signs of wear or fatigue, and the hydraulic system needed only two bleeds across the testing cycle to maintain full performance.