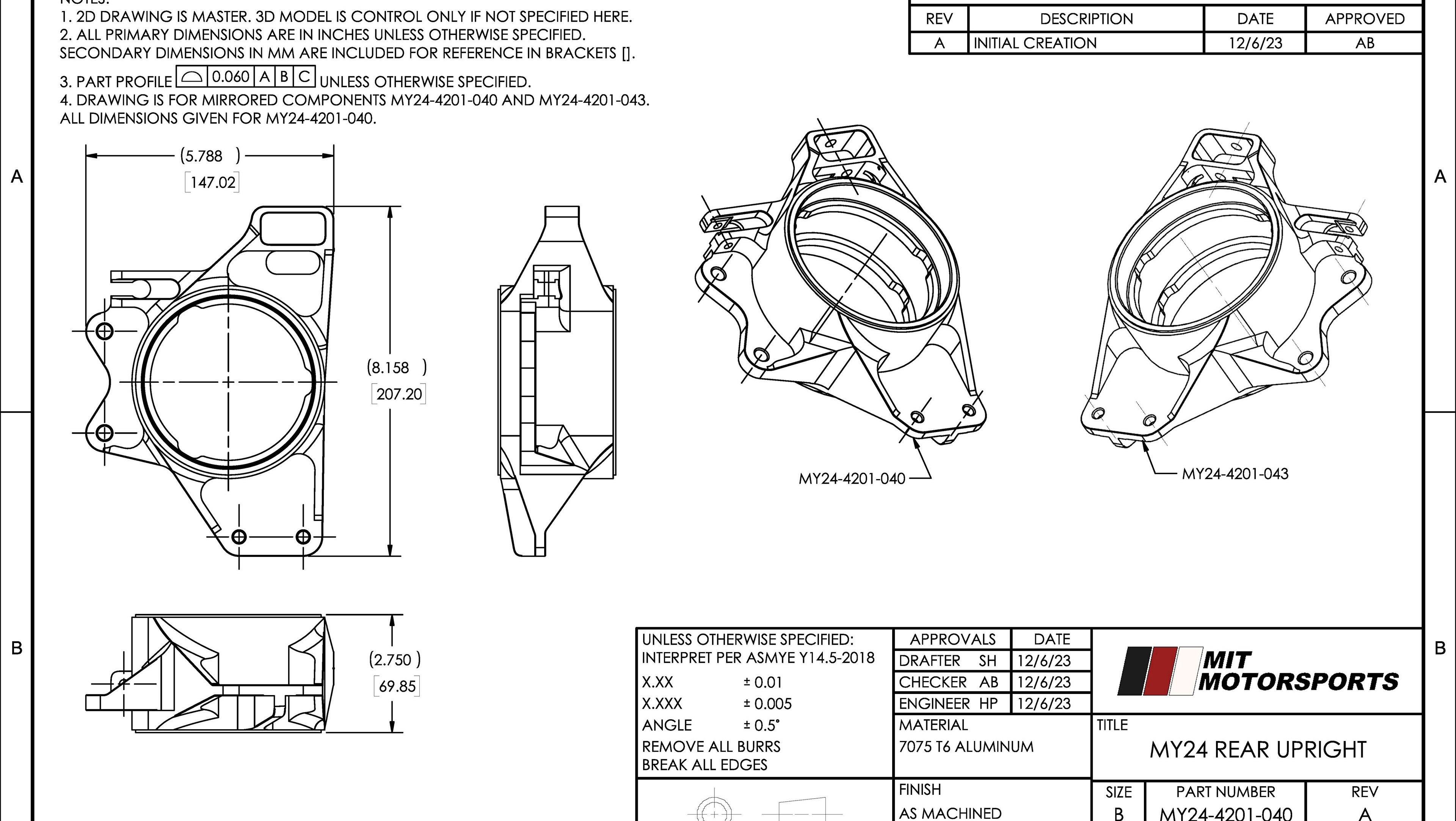
A key challenge for underwater navigation is the lack of access to traditional navigational systems such as GPS. To maintain bearing while underwater for extended periods of time, submarines use inertial navigation systems, integrating multiple gyroscopes and accelerometers to measure changes of angle and acceleration, then integrating to find changes in position over time. This navigation is especially important for ballistic missile submarines, such as the US' Ohio Class SSBNs. The accuracy of SLBMs, or submarine launched ballistic missiles, is heavily reliant on the accuracy of their initial position. To determine how accurate this initial positioning is, we can model the accuracy of inertial navigation systems over time. These systems are subject to compounding errors, or drift, over long periods of time from sources such as random errors and gyroscopic procession over time.
We begin with a document from Lucas Arthur of the MIT Laboratory for Nuclear Security and Policy. These equations will be used to calculate the development of error over time. First we calculate the rate at which uncertainty in orientation in each direction in the coordinate plane. We then integrate these rates of uncertainty growth to find the uncertainty at a specific moment in time.
The other important component of positional error is velocity, which we find by integrating the error in acceleration, a known property of the accelerometer.
Using equations 1.6, we can then turn the uncertainties in total velocity and each of the directional uncertainties to find the total velocity uncertainty in each direction. These uncertainties can finally be integrated to find the positional uncertainties in the x, y, and z planes.
This is where we code the equations to model uncertainty over time.
First we calculate the error in acceleration measurements, a function of constant bias in the accelerometers as well as a scalar multiple of the input acceleration. For simplification of the model, we assume the submarine is traveling at a constant velocity, causing the only acceleration error to be from constant bias.
We then create a function for each of the three principal directions to give the accumulation of error as a function of time. Creating these as a function of time will allow integration later on in the program.
For the equations to calculate total error, we use the quad function of the scipy library to carry out integration. We integrate our rate of accumulation equations as a function of time.
Before we can integrate each of the velocity and positional errors, we convert the total velocity into each of its components with trigonometric equations with the numpy library. These will be used with the velocity errors to find the positional errors.
We can now use our values for velocity error and orientation error to calculate the components of velocity error using equation 1.6 from the document above. integrating these values with the component velocities gives the positional error in each direction, demonstrating how error grows over time
The growth of positional error in the x direction, with a 150-day patrol cycle recalibrating the INS with GPS data every 30 days.
Interestingly, the code says there is no positional error in the Y direction over time, which intuitively seems incorrect. This is an area of potential further exploration to examine the Y-uncertainty equations and whether they are an accurate model, and whether my code implements them correctly.
The positional error in the z direction also seems far greater than intuitively makes sense. 300,000 kM error over 30 days is clearly far more than submarines experience, as this would be so great navigation would be effectively impossible. This is likely in large part due to the inherent inaccuracies in the gyroscopic property assumptions given the lack of public data. Further investigation is warranted similar to the Y-error to validate the implementation of the original equations to minimize possible errors to only data outside my control.